Série 4

Question

Construisez un décodeur 5-vers-32 en utilisant quatre décodeurs 3-vers-8 avec entrée enable.

Réponse

Question

Vous devez concevoir un encodeur à priorité à quatre entrées. L’entrée \(D_0\) doit avoir la plus grande priorité et l’entrée \(D_3\) doit avoir la plus faible priorité, avec la priorité des autres entrées qui suivent le même ordre. Les sorties seront \(s_1, s_0\) et \(v\) qui indique la validité des sorties: \(v=0\) si toutes les entrées sont à 0; \(v=1\) si au moins une entrée est 1.

Réponse

Question

Un circuit séquentiel à deux bascules D, \(A\) et \(B\), comporte deux entrées \(x\) et \(y\) et une sortie \(z\). Les équations de prochain état sont:

\[A_{n+1} = x^\prime y + x A\] \[B_{n+1} = x^\prime B + x A\]

L’équation de sortie est

\[z=B\]

1. Dessinez le schéma logique du circuit

2. Déterminez le tableau d’états

3. Dessinez le diagramme d’état

Réponse

1. Schéma logique

   

2. Tableau d’états

État présent	\(X\)	\(Y\)	État suivant	\(Z\)
0	0	0	0	0
0	0	1	1	0
0	1	0	0	0
0	1	1	0	0
1	0	0	0	0
1	0	1	1	0
1	1	0	2	1
1	1	1	2	1
2	0	0	3	1
2	0	1	2	1
2	1	0	2	1
2	1	1	2	1
3	0	0	3	1
3	0	1	2	1
3	1	0	0	0
3	1	1	0	0

1. Diagramme d’état

   

Question

Considérez le circuit logique suivant:

1. Quelle est la fonction combinatoire réalisée par la section logique combinatoire, c’est-à-dire, quelle est la fonction \(S = f(A,B)\) ?

2. Complétez le diagramme temporel de la figure, en supposant un temps de propagation maximum de 10 ns pour les portes NOR et OU, et de 40 ns pour les bascules.

3. Si les temps de maintien \(t_{h}\) et de prépositionnement \(t_{su}\) sont de 5 ns pour toutes les bascules, quelle est la fréquence maximale d’horloge utilisable pour que le circuit fonctionne convenablement? Utilisez un diagramme temporel pour évaluer la période minimum.

Réponse

1. Fonction combinatoire \(S = A \oplus B\)

2. Diagramme temporel

   

3. Analyse pour la période minimale

   La période minimale de l’horloge est de $40ns + 3\times 10ns + 5ns = 75ns$.

Question

Analysez le circuit logique suivant:

1. Analysez le comportement du circuit, en supposant qu’au départ les entrées sont \(A=0\) et \(B=0\) et la sortie \(S=0\). Vous devez supposer des changements des valeurs d’entrées et décrire les changements des sorties, en tenant compte de la mémoire du circuit.

2. Identifiez la fonction des entrées \(A\) et \(B\).

3. Identifiez la fonction du circuit.

Réponse

1. Fonction

   \(A = 0\)	\(B = 0\)	\(S = 0\)
   \(A = 1\)	\(B = 0\)	\(S = 0\)
   \(A = 1\)	\(B = 1\)	\(S = 1\)
   \(A = 1\)	\(B = 0\)	\(S = 1\)
   \(A = 1\)	\(B = 1\)	\(S = 1\)
   \(A = 0\)	\(B = 1\)	\(S = 0\)
   \(A = 1\)	\(B = 1\)	\(S = 1\)

1. \(A\) sert d’entrée de données, \(B\) sert d’entrée de contrôle.

2. Le circuit se comporte comme un loquet D.

Question

Considérez circuit séquentiel décrit par le diagramme d’état suivant:

1. En utilisant l’assignation d’états \(a = 00, b = 01, c = 10, d = 11\), construisez le tableau d’état pour ce circuit séquentiel.

2. Concevez le circuit en utilisant des portes standards et des bascules D.

Réponse

1. Tableau d’état

   État présent	\(X\)	État suivant	\(Z\)	\(F\)
   00	0	00	0	0
   00	1	01	0	1
   01	0	10	0	0
   01	1	11	1	0
   10	0	00	0	0
   10	1	11	0	0
   11	0	11	1	1
   11	1	11	1	1

1. Circuit

   

Question

Vous devez concevoir un circuit logique séquentiel à une entrée et une sortie qui identifie les deux séquences d’entrée 0110 et 11111 appliquées immédiatement après une remise à zéro asynchrone du circuit. Donnez le diagramme d’état simplifié pour ce circuit.

Réponse

Question

Vous devez concevoir un circuit logique séquentiel à une entrée et une sortie qui identifie les deux séquences d’entrée 0110 et 11111. Les séquences d’entrée doivent être identifiées à n’importe quel moment où elles apparaissent en entrée.

Réponse

Question

Déterminez le diagramme d’état pour un circuit séquentiel synchrone avec une entrée \(x\) et une sortie \(z\) qui est utilisé pour reconnaître la séquence d’entrée 101. La sortie doit donc être \(z=1\) lorsque le dernier 1 de la séquence 101 est identifié. \(z\) est ensuite remis à zéro au prochain coup d’horloge. Les chevauchements de 101 ne sont pas permis. Par exemple,

\[x = 010101101\] \[z = 000100001\]

Réponse

Question

Concevez le circuit séquentiel synchrone décrit par le diagramme d’état ci-dessous. Vous devez considérer des bascules JK et D et choisir la solution la plus simple. Présentez clairement toutes les étapes, jusqu’au schéma du circuit correspondant.

État courant	Entrée	Prochain état	Sortie
00	0	01	0
00	1	11	0
01	0	10	0
01	1	00	1
11	0	00	1
11	1	10	0
00	0	10	1
00	1	01	1

Réponse

Question

Les deux bascules du circuit suivant sont activées par les transitions montantes du signal présent à leur entrée d’horloge.

Tracez le chronogramme pour \(X, X^\prime, Y, S\)

Réponse

Question

Vous devez analyser le circuit séquentiel suivant:

1. Donnez les équations pour le décodeur de prochain état.

2. Donnez le tableau d’activation avec état présent, entrée, entrées des bascules, prochain état, sortie.

3. Donnez le diagramme d’état correspondant.

4. Tracez le chronogramme de fonctionnement, en faisant abstraction des délais de propagation.

5. En sachant que la bascule a les caractéristiques suivantes:

   • temps de pré-positionnement minimum: 11 ns

   • temps de maintien minimum: 9 ns

   • temps de propagation maximum: de Horloge à \(Q\) ou \(Q^{\prime}\): \(t_{pLH}\) = 15 ns, \(t_{pHL}\) = 13 ns.

   et en supposant un délai de propagation de 15 ns pour la porte XOR, déterminez la période minimale et la fréquence maximale qu’on puisse utiliser tout en étant assuré que le circuit fonctionne correctement. Donnez les détails de votre raisonnement.

Réponse

1. \[S^{n+1} = (A(S^n)^{\prime}) + (B^{\prime} S^n)\]

2. Tableau d’activation

   \(B\)	\(A\)	\(S^n\)	\(S^{n+1}\)	\(S\)
   0	0	0	0	0
   0	0	1	1	1
   0	1	0	1	0
   0	1	1	1	1
   1	0	0	0	0
   1	0	1	0	1
   1	1	0	1	0
   1	1	1	0	1

1. Diagramme d’état

   

2. Chronogramme

   

3. Analyse temporelle

   

   La période minimale est de \(15 ns+15 ns+11 ns = 41 ns\).

Question

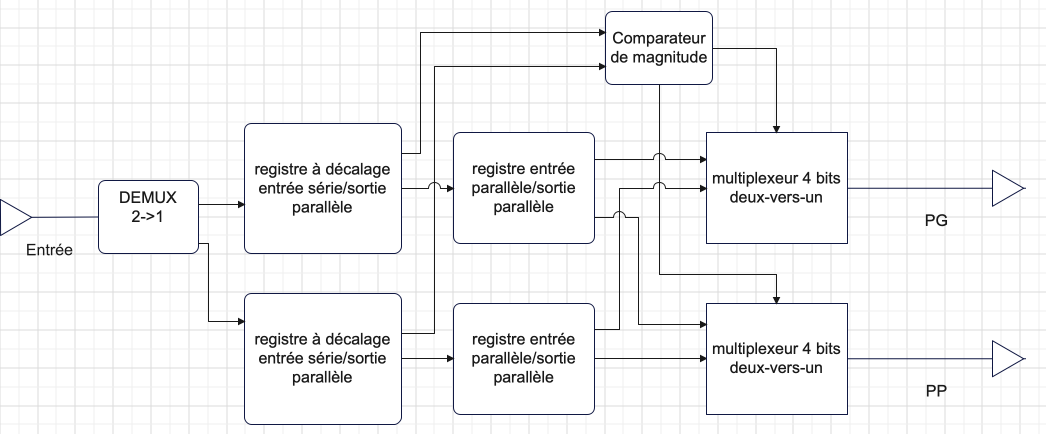
Vous devez concevoir un circuit logique utilisé dans un système permettant de trier des données. Le circuit reçoit deux nombres non-signés de 4 bits, multiplexés en série sur une même entrée. Par exemple, si les entrées sont \(1010\) et \(1110\), le circuit recevra \(11011100\). Le circuit doit acheminer le plus grand des deux nombres à une sortie (parallèle) appelée PG et le plus petit à une sortie (parallèle) appelée PP. Vous devez réaliser votre circuit en utilisant les éléments suivants:

• démultiplexeur un-vers-deux

• multiplexeur 4 bits deux-vers-un (il s’agit de quatre multiplexeurs deux-vers-un à un bit avec le même signal de commande, et qui traitent ainsi en parallèle des mots de quatre bits)

• registre à décalage entrée série/sortie parallèle

• comparateur de magnitude: deux entrées parallèles de 4 bits: \(A\) et \(B\), trois sorties: \(A\geq B\), \(A=B\), \(A \leq B\)

• registre entrée parallèle/sortie parallèle

Donnez un schéma-bloc de votre circuit en indiquant seulement les blocs qui traitent les données (pas les blocs qui serviront à contrôler le circuit).

Réponse

Question

On doit concevoir un système séquentiel avec une entrée \(E\) et une sortie, et qui génère les séquences de sortie suivantes:

• si \(E=0\), séquence de sortie = 1100, périodique

• si \(E=1\), séquence de sortie = 1011, périodique

On envisage deux versions du système:

version 1
si \(E\) change, la séquence de sortie suit le changement au vol.

version 2
si \(E\) change, la séquence de sortie recommence à partir du début.

Par exemple,

Entrée	1	1	1	1	0	0	0	0	0	1	1	1	0	0
Sortie version 1	1	0	1	1	1	1	0	0	1	0	1	1	1	1
Sortie version 2	1	0	1	1	1	1	0	0	1	1	0	1	1	1

Donnez un diagramme d’état pour chacune des deux versions.

Réponse

1. Diagramme d’état, version 1

   

2. Diagramme d’état, version 2

   

Question

Considérez le tableau d’état suivant:

État présent	Entrée \(A\)	État suivant	Sortie \(S\)
a	0	c	1
a	1	a	1
b	0	e	0
b	1	f	1
c	0	b	1
c	1	d	0
d	0	a	0
d	1	b	1
e	0	e	0
e	1	f	1
f	0	c	1
f	1	f	1

correspondant à un circuit séquentiel synchrone.

1. Simplifiez ce tableau d’état en identifiant les états équivalents, en utilisant la méthode du tableau d’implication.

2. Donnez le diagramme d’état simplifié correspondant au tableau d’état simplifié. Nommez les états simplifiés qui restent a, b, c, …

3. Assignez des codes aux états, en commençant avec la représentation binaire de 0 pour a, de 1 pour b, etc.

4. Donnez les diagrammes de Karnaugh pour le décodeur de prochain état en supposant des bascules JK, et les fonctions simplifiées correspondantes.

5. Donnez le diagramme de Karnaugh pour le décodeur de sortie.

6. Dessinez le schéma du circuit séquentiel obtenu.

Réponse

1. Tableau d’implication

b		X	–	–	–	–
c		X	X	–	–	–
d		X	XX	X	–	–
e		X	OUI	X	XX	–
f		OUI	X	X	X	X
		a	b	c	d	e

1. Tableau d’état, assignation d’états et diagramme d’état

État présent	Entrée \(A\)	État suivant	Sortie \(S\)
a	0	c	1
a	1	a	1
b	0	b	0
b	1	a	1
c	0	b	1
c	1	d	0
d	0	a	0
d	1	b	1

État	Code
a	00
b	01
c	10
d	11

1. Diagrammes de Karnaugh, décodeur de prochain état

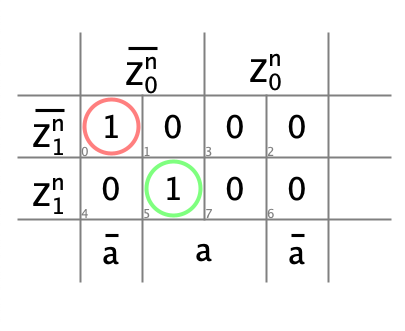
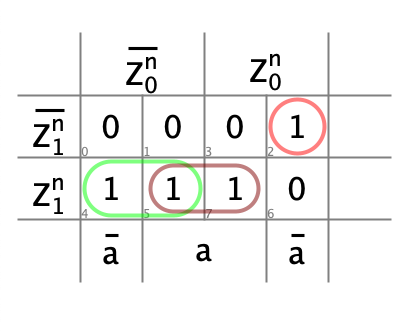
1. Diagrammes de Karnaugh, décodeur de sortie

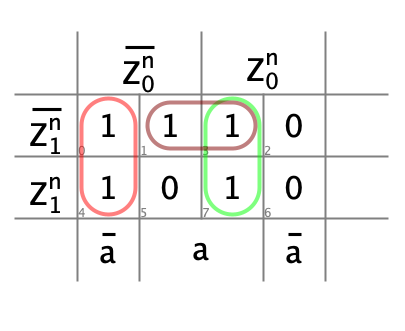
1. Schéma du circuit

Question

Considérez le circuit séquentiel synchrone ci-dessous.

Déterminez la vitesse d’horloge maximale en considérant les caractéristiques suivantes:

• Portes: temps de propagation maximum: 10 ns.

• Bascules: temps de mise en place minimum: 12 ns.

• Bascules: temps de maintien minimum: 15 ns.

• Bascules: temps de propagation maximum: de H à \(Q\) ou \(Q^{\prime}\): \(t_{pLH}\) = 25 ns, \(t_{pHL}\) = 20 ns.

Réponse

La période minimale de l’horloge est de \(25ns + 2\times 10ns + 12ns = 57ns\).

---