Compléments de nombres
Les compléments de nombres jouent un rôle dans la simplification de certaines opérations mathématiques et logiques. Dans un système de numération de base \(b\), on considère deux types de compléments: le complément à \(b\) et le complément à \(b-1\). Pour la base 10, nous aurons donc le complément à dix et le complément à neuf. Pour les nombres binaires (base 2), nous aurons le complément à deux et le complément à un. Pour évaluer les compléments d’un nombre, on doit tenir compte du nombre de chiffres que comporte ce nombre.
Complément à neuf et complément à un
Soit un nombre entier \(N\) en base \(b\) constitué de \(n\) chiffres. Le complément à \(b-1\) de \(N\) est \((b^n-1)-N\).
Par exemple, en base \(b=10\), le complément à neuf pour le nombre décimal \(N = 4576\) formé de \(n=4\) chiffres sera \((b^n-1)-N = (10^4 -1) - 4576 = 5424\).
En base \(b=2\), le complément à un pour le nombre binaire \(N = (10011)2 = (19)10\) formé de \(n=5\) bits sera \((b^n-1)-N = (2^5 -1) - 19 = 12\) ce qui donne en binaire: \((12)10 = (1100)2\).
On peut vérifier qu’il est très facile, en binaire, de déterminer le complément à un, sans effectuer de calculs, en inversant simplement chacun des bits de la représentation binaire du nombre à complémenter. Ainsi, avec notre exemple, on trouve:
\[10011\] \[01100\]Remarquons ici un zéro non significatif comme premier bit à gauche.
Complément à dix et complément à deux
Le complément à \(b\) de l’entier \(N\) s’évalue comme \((b^n)-N\). Cela correspond à ajouter 1 au complément à \(b-1\).
Ainsi, pour notre exemple précédent en base \(b=10\), le complément à dix pour le nombre décimal \(N = 4576\) formé de \(n=4\) chiffres sera \((b^n)-N = (10^4) - 4576 = 5425\).
Pour notre autre exemple, en base \(b=2\), le complément à deux pour le nombre binaire \(N = (10011)2 = (19)10\) formé de \(n=5\) bits sera \((b^n)-N = (2^5) - 19 = 13\) ce qui donne en binaire: \((13)10 = (1101)2\).
L’évaluation directe à la main, sans calculs, du complément à deux est également possible en suivant la démarche suivante:
- On parcourt le nombre binaire initial à partir (à droite) du bit le moins significatif, en retranscrivant les bits rencontrés jusqu’à atteindre un premier bit 1, que l’on retranscrit également.
- On continue la retranscription vers la gauche, en inversant cette fois les bits subséquents.
Par exemple, pour (10110)2, on aura la démarche détaillée dans le tableau 8. Les étapes sont numérotées selon la position considérée, à partir de la droite.
| nombre | 1 | 0 | 1 | 1 | 0 | |
|---|---|---|---|---|---|---|
| Étape 0 | 0 | Retranscrit | ||||
| Étape 1 | 1 | 0 | Retranscrit | |||
| Étape 2 | 0 | 1 | 0 | Inversé | ||
| Étape 3 | 1 | 0 | 1 | 0 | Inversé | |
| Étape 4 | 0 | 1 | 0 | 1 | 0 | Inversé |
Pour une évaluation par un circuit, on commencera par déterminer le complément à un par inversion et on lui additionnera 1 pour obtenir le complément à deux.
Nombres signés et codage
Représenter des nombres \(\geq 0\) en binaire est donc relativement naturel. Dans l’optique où on voudra stocker ces nombres dans une mémoire binaire numérique, il n’y a qu’à prévoir une taille suffisante (en nombre de bits) pour pouvoir accommoder des nombres assez grands pour l’application considérée. Avec \(n\) bits, il est possible de représenter des entiers de 0 à \(2^n-1\) avec cette représentation «naturelle».
Mais on peut se demander comment représenter des nombres négatifs, c’est-à-dire \(< 0\). Une première observation est le fait que si on considère des nombres positifs et négatifs, on double en quelque sorte la quantité de valeurs à représenter. Par exemple, il y a 21 nombres à représenter si on veut pouvoir utiliser les valeurs comprises entre \(-10\) et \(+10\), comme on peut le voir dans le tableau 9.
| Gamme | N. de valeurs |
|---|---|
| de -10 à -1 | 10 |
| 0 | 1 |
| de 1 à 10 | 10 |
| Total | 21 |
Nous devons donc nous assurer d’avoir autant de combinaisons de bits qu’il sera nécessaire. La deuxième observation est qu’il faudra un moyen de distinguer les nombres positifs des nombres négatifs. Si on veut que cette distinction puisse se faire non seulement sur papier, mais surtout lorsque les nombres seront stockés et manipulés dans un système électronique, il faut définir un format binaire «tout compris» qui permette de le faire.
Nous devons donc établir un code, c’est-à-dire une convention qui permettra de donner un sens à un groupe de bits. Le choix de la convention devrait être guidé par les usages qui seront ultimement faits des nombres qui seront représentés.
En fait, lorsque nous avons convenu (implicitement) de représenter des nombres entiers en utilisant directement la conversion en base 2 des nombres décimaux, nous avons établi un code de représentation qui, bien que naturel, n’en est pas moins une convention. Ici, nous devrons formuler plus explicitement la convention qui sera utilisée pour représenter les entiers signés.
Une convention de représentation peut être établie totalement arbitrairement, mais elle sera sans doute plus utile si elle peut contribuer à faciliter des opérations courantes réalisées avec les éléments à représenter. Puisqu’il est question ici de nombres entiers signés, l’opération à considérer en priorité est l’addition. Nous devrions aussi considérer les trois points suivants dans notre choix de convention pour attribuer des codes binaires aux valeurs. (Pour illustrer notre réflexion, nous allons considérer des nombres pouvant être représentés par des codes binaires de 4 bits, ce qui permet en théorie de représenter un total de 16 valeurs.)
-
Puisqu’il faudra partager notre ensemble de codes binaires en deux, il serait logique de placer la représentation pour zéro au centre de ce découpage.
-
Les codes binaires utilisés pour un nombre et pour son inverse additif devraient être disposés symétriquement autour du code utilisé pour représenter le zéro. Il est naturel de représenter la valeur zéro avec le code 0000.
-
L’ordre des codes devrait correspondre à l’ordre des nombres. On sait bien comment ordonner les nombres entiers, en passant des nombres négatifs aux nombres positifs.
Quel ordre serait approprié pour les représentations (codes binaires)? L’ordre naturel, du moins pour les nombres entiers positifs, serait de passer de 0000 à 0001 à 0010, etc. Il faudra cependant limiter le nombre de valeurs positives, car il faut réserver des codes pour les valeurs négatives, et nous avons déjà utilisé un code pour le zéro.
Quel code binaire devrait-on placer juste avant le zéro, pour représenter -1? Si on dispose l’ensemble des codes binaires entre 0000 et 1111 selon un cycle, comme illustré sur la figure suivante, alors le code approprié pour -1 sera 1111. Et le code pour -2 sera 1110. Un avantage de cette disposition est que, en ajoutant 1 pour passer de -2 à -1, on parcourt le cycle dans le même sens qu’en ajoutant 1 pour passer de 1 à 2.
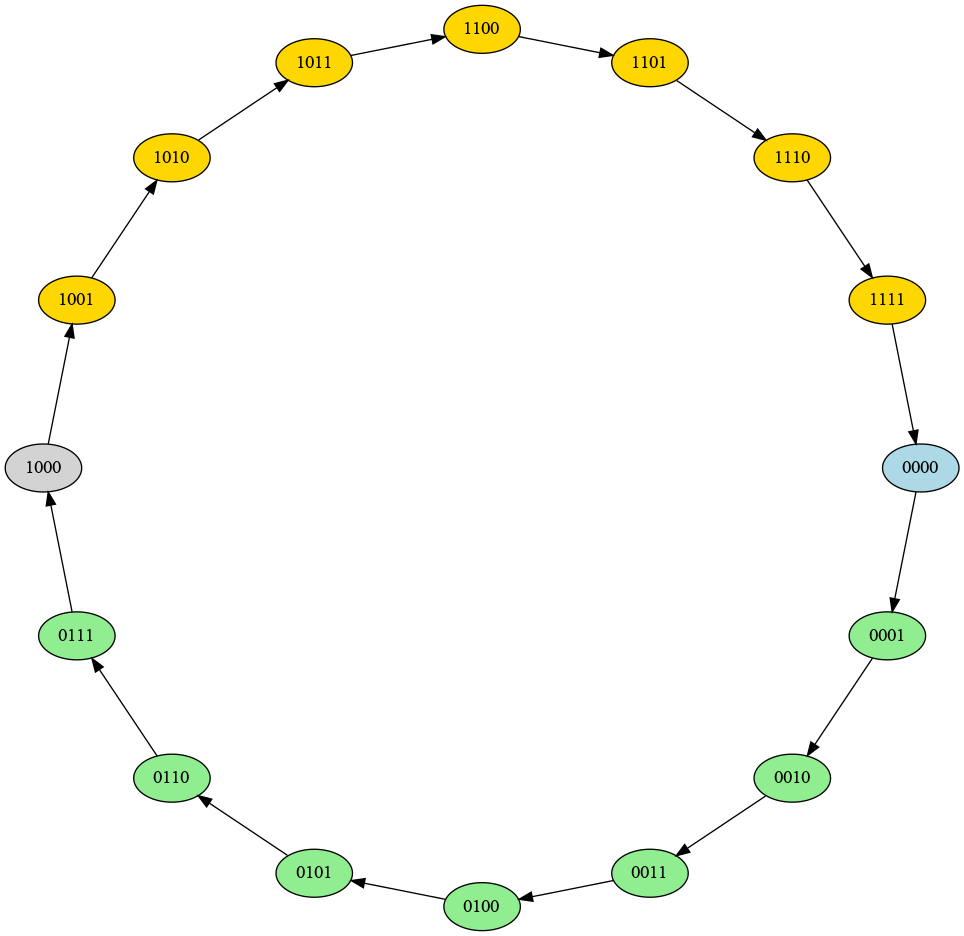Relations entre les codes dans l’assignation en complément à deux
En suivant cette logique, on pourra, comme indiqué sur la figure, assigner les codes dans les boîtes en ellipses, en jaune, à des valeurs positives et les codes dans les boîtes en hexagones, en vert, à des valeurs négatives. Si on assigne autant de valeurs positives que de valeurs négatives, un seul code binaire ne sera pas utilisable, le code 1000, dans la boîte en losange. Tout mouvement selon le sens des flèches (horaire) sur l’illustration correspond à une addition; tout mouvement en sens inverse correspond à une soustraction. Les nombres binaires seront ainsi symétriques par rapport à notre zéro.
Nous obtenons ainsi l’assignation du tableau 10.
| Code | Nombre |
|---|---|
| 1001 | -7 |
| 1010 | -6 |
| 1011 | -5 |
| 1100 | -4 |
| 1101 | -3 |
| 1110 | -2 |
| 1111 | -1 |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | aucun |
Voici quelques observations importantes sur cette représentation.
-
Tous les codes des nombres négatifs ont le premier bit à gauche (qui serait le bit le plus significatif) à la valeur 1, alors que les autres codes ont la valeur 0. Ce bit peut ainsi servir d’indicateur de signe, avec la convention habituelle qu’on ne met pas de signe au zéro. On parlera ainsi de bit de signe pour dénoter ce bit, qui ne contribue pas à la grandeur (en valeur absolue) du nombre.
-
L’inverse additif d’un nombre \(n\), c’est-à-dire \(-n\), est représenté par le complément à deux du nombre. Ceci signifie que pour trouver l’inverse additif d’un nombre, il suffit de calculer son complément à deux. Le complément à deux du complément à deux nous redonnera le nombre initial, conformément à la double négation \(--n = n\).
Il existe d’autres conventions pour la représentation de nombres signés, comme la représentation signe+magnitude, mais la représentation en complément à deux est de loin la plus utilisée.
Opérations arithmétiques binaires
Addition de nombres non signés
En transposant les opérations classiques pour effectuer à la main des additions ou des soustractions, il est possible d’effectuer des calculs avec des nombres binaires. Additionner des nombres entiers non signés ne pose pas de difficultés particulières.
On suppose deux nombres entiers binaires non signés \(A\) et \(B\) représentés en utilisant le même nombre de bits (si un nombre est plus petit, on ajoutera des 0 non significatifs à gauche pour compléter la représentation). Lorsqu’on effectue l’opération bit par bit, en partant de la position la moins significative, on peut utiliser la table d’addition suivante. À la position \(i\), on a trois entrées à prendre en considération: \(A_{i}\) et \(B_{i}\), les bits des nombres à additionner, et \(R_{i-1}\), la retenue provenant de la position \(i-1\). En sortie, on a la somme \(S_{i}\) et la retenue \(R_{i}\). On obtient le tableau de vérité suivant (11).
| $$A_{i}$$ | $$B_{i}$$ | $$R_{i-1}$$ | $$R_{i}$$ | $$S_{i}$$ |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Exemple:
A: 101110001 B: 001111001 S: 111101010 R: 001110001
S’il y a une retenue non nulle à la suite de l’addition à la position la plus significative, il y a un débordement, car le résultat est trop grand pour être représenté avec le nombre de bits initial.
Addition de nombres signés
L’addition de nombres signés codés avec la représentation en complément à deux est nettement avantageuse. Il suffit d’additionner les deux nombres comme s’il s’agissait de nombres non signés, en incluant les bits de signe dans le calcul. La retenue qui émane de la position la plus significative ne doit pas être prise en compte.
Exemple 1:
Additionnons \(A=-2\) et \(B=4\), représentés respectivement (1110)2 et (0100)2.
A: 1110 B: 0100 S: 0010 R: 1100
qui nous donne bien le résultat escompté: S = (0010)2 = (2)10.
Exemple 2:
Additionnons \(A=3\) et \(B=-5\), représentés respectivement (0011)2 et (1011)2.
A: 0011 B: 1011 S: 1110 R: 0011
qui nous donne bien le résultat escompté: S = (1110)2 = (-2)10.
On peut vérifier facilement qu’additionner un nombre avec son complément à deux donne toujours zéro, ce qui revient à faire \(-n + n = 0\).
Comme avec l’addition de nombres entiers non signés, il faudra se préoccuper des débordements qui peuvent survenir parce que la capacité de représentation est limitée par la taille (en nombre de bits) des codes binaires utilisés.
Soustraction de nombres signés
La soustraction s’effectue en faisant \(A - B = A + (-B)\), comme suit:
- On détermine le complément à deux du nombre à soustraire (ici, \(B\)).
- On additionne ce complément à deux au nombre duquel on soustrait (ici, \(A\)). La retenue qui émane de la position la plus significative ne doit pas être prise en compte.
Le résultat s’interprétera comme un nombre signé en complément à deux.
Extension de signe
Dans la représentation des nombres signés en complément à deux, le bit de signe (bit le plus à gauche) est une indication directe du signe d’un nombre. Si on change la taille des nombres, c’est-à-dire, le nombre de bits utilisés au total pour la représentation, il faut une opération spécifique pour préserver l’encodage en complément à deux.
Considérons par exemple le nombre 5, représenté d’abord sur quatre bits et ensuite sur huit bits. On a pour 5
\[0101\]ou encore
\[00000101\]Quand on compare ces deux représentations, on observe:
- qu’elles se terminent de la même façon, avec les trois bits 101 qui représentent la grandeur du nombre;
- que le bit le plus à gauche est 0 dans les deux cas (même signe);
- que dans la représentation sur huit bits, il y a des bits 0 entre le bit de signe et les trois derniers bits.
Considérons maintenant un nombre négatif, le nombre -5, représenté d’abord sur quatre bits et ensuite sur huit bits. Le complément à deux de 5 = (0101)2 est
\[1011\]alors que le complément à deux de 5 = (00000101)2 est
\[11111011\]Quand on compare ces deux représentations, on observe:
- qu’elles se terminent de la même façon, avec les trois bits 011;
- que le bit le plus à gauche est 1 dans les deux cas (même signe);
- que dans la représentation sur huit bits, il y a des bits 1 entre le bit de signe et les trois derniers bits.
Ces constatations nous amènent à conclure que lorsqu’on augmente la taille de représentation d’un nombre signé, il faut faire une extension de signe pour intercaler les bonnes valeurs binaires entre le bit de signe et les bits qui représentent la grandeur du nombre. Pour un nombre positif, on doit intercaler des bits 0, alors que pour un nombre négatif, on intercale des bits 1. On peut donc énoncer la règle comme on doit intercaler des bits dont la valeur est la même que le bit de signe.
Si, à l’inverse, on réduit la taille des nombres signés, on n’aura qu’à supprimer des bits, tous égaux au bit de signe, entre le bit de signe et ceux qui représentent la grandeur du nombre. Si les bits à supprimer ne sont pas tous égaux au bit de signe, c’est une indication que la réduction de taille n’est pas possible: la nouvelle taille est insuffisante pour représenter les nombres correctement.
Codes binaires
Il n’y a pas que des nombres que l’on voudra représenter en binaire. Il est maintenant le temps de définir ce qu’on appelle un code binaire, car cette notion est au centre de tous les encodages que nous aurons à utiliser.
Un code binaire sur \(n\) bits est typiquement une association entre, d’une part, les éléments d’un ensemble que l’on cherche à représenter et d’autre part, les différents groupes ou patrons possibles avec \(n\) bits. On appelle parfois ces patrons des mots du code (ou par abus de langage, des codes). Comme il y a \(2^n\) patrons de bits différents, il est possible d’associer jusqu’à ce nombre d’éléments.
Une règle, souvent implicite mais essentielle, stipule qu’on ne devrait associer qu’un seul élément à un patron de bits donné. Sinon, l’interprétation du code (le décodage) devient ambiguë. Selon l’application, il n’est pas toujours nécessaire d’associer tous les patrons de bits à des éléments. Par exemple, si on veut représenter les chiffres décimaux, il est nécessaires de disposer d’au moins 10 patrons de bits, ce qui est possible avec \(n=4\). Puisque \(2^4 = 16\), il y aura \(16 - 10 = 6\) patrons de bits inutilisés.
La règle spécifique d’association peut être établie arbitrairement, mais elle est souvent conçue en vue de respecter certaines propriétés liées aux éléments à représenter ou à la configuration du code lui-même. C’est ce qu’on a fait, par exemple, pour définir la convention d’encodage des entiers par complément à deux.
Code Gray
Lorsqu’on utilise un code binaire pour représenter des valeurs associées à des phénomènes physiques, il peut être opportun d’utiliser un encodage dans lequel le nombre de changements de bits est minimal lorsqu’on passe d’un patron de bits au suivant dans la séquence des codes. Par exemple, si on cherche à encoder des positions d’un interrupteur rotatif (comme pour encoder des angles), il est préférable que lorsqu’on passe d’une position à la suivante en tournant le commutateur, un seul bit ne change dans la sortie. Ainsi, une erreur sur un bit n’introduit pas un gros changement dans l’interprétation de la valeur encodée. Un code Gray permet d’atteindre cet objectif.
Avec le code Gray du tableau 12, on peut voir par exemple que la transition entre les codes pour 7 et 8 n’entraîne qu’un changement sur un bit, de 0110 à 1100. Avec un encodage classique basé sur les entiers binaires, on aurait observé pour ce cas une transition entre 0111 et 1000, qui comporte quatre changements de valeurs de bits.
| Code Gray | Valeur |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0011 | 2 |
| 0010 | 3 |
| 0110 | 4 |
| 0111 | 5 |
| 0101 | 6 |
| 0100 | 7 |
| 1100 | 8 |
| 1101 | 9 |
| 1111 | 10 |
| 1110 | 11 |
| 1010 | 12 |
| 1011 | 13 |
| 1001 | 14 |
| 1000 | 15 |
Codes alphanumériques et autres
Vous rencontrerez sans doute plusieurs autres encodages courants, par exemple pour encoder des caractères (code ASCII, codes UTF) ou pour encoder uniquement des chiffres décimaux (code BCD). Une fois qu’on a bien compris la règle d’encodage, il n’y a généralement pas de difficultés à les utiliser.
Certains codes sont construits de manière à permettre d’identifier et même, dans certains cas, de corriger des erreurs dans le stockage ou la transmission des données encodées. Ces codes sont construits en fonction de règles d’encodage, qui, lorsqu’elles ne sont pas respectées, permettent de constater la présence d’erreurs.