Additionneur binaire pour \(n\) bits
Un additionneur binaire est un circuit logique qui permet d’évaluer la somme arithmétique de deux nombres binaires de \(n\) bits. Il peut être conçu en combinant des additionneurs complets en cascade, en reliant la retenue de sortie provenant de la position 0 (la moins significative) à l’entrée de retenue de la position 1, la retenue de sortie provenant de la position 1 à l’entrée de retenue de la position 2,…, la retenue de sortie provenant de la position \(i-1\) à l’entrée de retenue de la position \(i\), etc. (figure ci-dessous).
Pour en faire un circuit général pouvant également se combiner en chaîne, on prévoit une entrée pour une retenue au niveau 0, \(r_0\) et une sortie pour une retenue du dernier niveau \(n-1\), \(R_{n-1}\). On doit donc, pour le chaînage, acheminer la sortie retenue du niveau courant à l’entrée de retenue du niveau suivant.
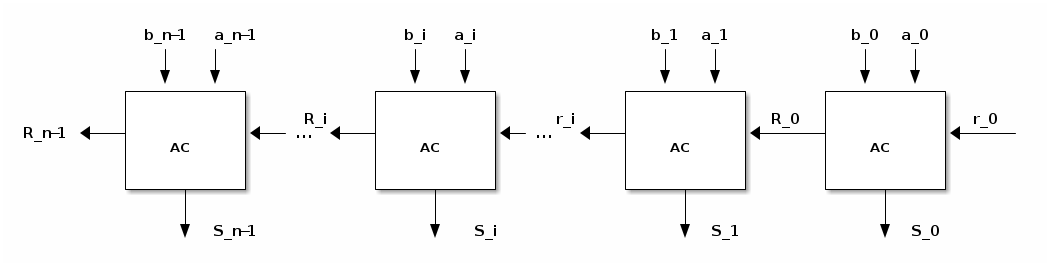Chaîne d’addition
Cette réalisation en forme de chaîne, en réutilisant de façon systématique un bloc élémentaire, est avantageuse du point de vue de la complexité et de la flexibilité. Imaginons par exemple le défi de concevoir un additionneur binaire pour des nombres de quatre bits avec la méthode classique. Comme il faudrait considérer neuf entrées, le tableau de vérité comporterait \(2^9= 512\) lignes!
Propagation de retenue
L’approche en cascade ne comporte pas que des avantages. Lorsqu’on effectue l’addition de deux nombres, les bits d’entrée des deux arguments et la retenue d’entrée sont présentés en même temps à l’additionneur. Comme dans tout circuit combinatoire, il faut un certain délai avant que les sorties n’atteignent leur niveau de sortie final. Ce délai de propagation dépend de la profondeur du circuit, en nombre de portes élémentaires à franchir de l’entrée vers la sortie. Et c’est évidemment le chemin le plus long qui détermine le délai de propagation global.
Dans le cas de l’additionneur, le chemin de propagation le plus long est celui qui mène à la dernière retenue finale \(R_{n-1}\). En effet, pour pouvoir calculer \(R_{n-1}\), bien que les valeurs de \(a_{n-1}\) et \(b_{n-1}\) soient déjà disponibles, il faut attendre que la valeur de \(r_{n-1} = R_{n-2}\) soit stabilisée avant que le calcul puisse s’effectuer avec les bonnes valeurs. Il en est de même avec le bloc précédent et ainsi, en remontant la chaîne vers \(r_0\), on trouve le chemin de propagation de retenue comme chemin le plus long.
Pour déterminer le nombre de portes à franchir pour le chemin de propagation de retenue, nous avons ajouté deux sorties intermédiaires à notre circuit d’additionneur complet, \(P_i\) et \(G_i\), permettant de récrire la sortie comme \(S_i = P_i \operatorname{Xor} r_i\) et la retenue de sortie comme \(R_i = P_i r_i + G_i\). Les signaux \(P_i\) et \(G_i\) ne dépendent que des entrées et sont donc disponibles après le délai des portes ET et XOR. Le chemin de \(r_i\) à \(R_i\) passe par une porte ET et une porte OU. Pour un additionneur de \(n\) bits comprenant \(n\) additionneurs complets, on aura une profondeur de retenue totale de \(2n\) portes.
Circuit additionneur complet montrant les signaux intermédiaires \(P_i\) et \(G_i\)
Anticipation de retenue
Les valeurs calculées par le circuit complet en chaîne ne seront valides et ne devront être prises en compte que lorsque le délai maximal se sera écoulé. Entre-temps, les valeurs binaires présentes aux différentes sorties assumeront typiquement des valeurs changeantes jusqu’à la stabilisation finale. Le délai de propagation de retenue est un facteur qui limite la vitesse à laquelle on pourra calculer la somme de deux nombres. Et comme l’addition est une opération souvent utilisée, parfois à répétition, pour réaliser d’autres opérations arithmétiques, cette limitation est problématique.
Il serait en théorie possible de ramener à un minimum le délai de calcul de la retenue finale en réalisant cette fonction en deux niveaux, par exemple avec un produit de sommes. Cette option n’est pas réaliste, car le nombre d’entrées à considérer en parallèle est prohibitif.
Comme solutions de compromis intermédiaires, un certain nombre de mécanismes ont été élaborés, dont l’approche par anticipation de retenue, que nous allons explorer ici. On fait appel aux deux signaux \(P_i = a_i \operatorname{Xor} b_i\) et \(G_i = a_i b_i\), qui donnent respectivement pour la sortie et la retenue de sortie
\[S_i = P_i \operatorname{Xor} r_{i-1}\] \[R_i = P_i r_{i-1} + G_i\]\(G_i\) est le signal qui indique la génération de retenue, produisant une retenue lorsque \(a_i\) et \(b_i\) sont tous deux à 1, sans égard à la valeur de la retenue d’entrée \(r_{i-1}\). Le signal \(P_i\) est l’indicateur de propagation de retenue, parce qu’il détermine si la retenue du niveau précédent \(r_{i-1}\) sera propagée à \(R_i\).
En partant du niveau 0, voici les expressions pour les différentes retenues:
\[R_0 = r_0 = \operatorname{in}\] \[R_1 = G_0 + P_0 R_0\] \[R_2 = G_1 + P_1 R_1 = G_1 + P_1 (G_0 + P_0 R_0) = G_1 + P_1 G_0 + P_1 P_0 R_0\] \[R_3 = G_2 + P_2 R_2 = G_2 + P_2 G_1 + P_2 P_1 G_0 + P_2 P_1 P_0 R_0\]etc.
Les expressions pour les retenues successives sont en forme somme de produits, ce qui mène à une implémentation à deux niveaux pour calculer les retenues rapidement. Contrairement à l’approche de propagation de retenue, toutes les retenues sont obtenues après un même délai équivalent à une profondeur de deux portes. En calculant d’abord les différentes valeurs de \(P_i\) et \(G_i\) pour chaque niveau et en utilisant ces résultats intermédiaires pour, d’une part, alimenter le circuit d’anticipateur de retenue et, d’autre part, effectuer \(S_i = P_i \operatorname{Xor} r_i\), on obtient un additionneur parallèle plus rapide que la configuration en cascade.
Circuit d’anticipateur de retenue pour \(n= 4\)