Circuits logiques combinatoires classiques
Nous allons maintenant nous intéresser à un certain nombre de fonctions typiques que l’on rencontre fréquemment en circuits logiques. Ce sera aussi l’occasion de mettre en pratique les approches de conception que nous avons vues.
Additionneur binaire
Une des opérations binaires les plus utilisées est l’addition (et la soustraction). Nous avons présenté à la section Compléments le tableau de vérité pour un additionneur binaire dont les entrées sont \(a_{i}\) et \(b_{i}\), les bits des nombres à additionner etaussi \(r_{i-1}\), la retenue provenant de la position \(i-1\). En sortie, on a la somme \(S_{i}\) et la retenue \(R_{i}\). Notez que pour bien distinguer la retenue d’entrée de la retenue de sortie, nous utilisons un symbole minuscule, \(r_{i-1}\), pour l’entrée et un symbole majuscule, \(R_{i}\), pour la sortie.
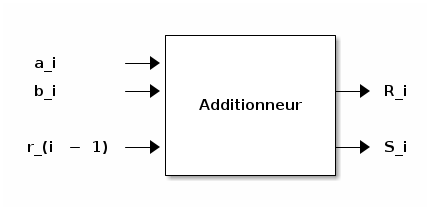Schéma-bloc d’un additionneur complet
| $$a_{i}$$ | $$b_{i}$$ | $$r_{i-1}$$ | $$R_{i}$$ | $$S_{i}$$ | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 |
Demi-additionneur
Un circuit logique qui effectue l’addition de deux bits est appelé un demi-additionneur. Mais ce qu’il nous faut vraiment, c’est un additionneur complet, c’est-à-dire un circuit de trois entrées qui fait l’addition de trois bits, puisqu’il faudra pouvoir tenir compte de la retenue du niveau précédent pour effectuer l’addition sur un niveau. Il est possible d’implémenter l’additionneur complet avec deux demi-additionneurs.
| $$a_{i}$$ | $$b_{i}$$ | $$R_{i}$$ | $$S_{i}$$ | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
À partir du tableau de vérité, on peut trouver que \(S_{i} = a_i b_i^\prime + a_i^\prime b_i = a_i \operatorname{Xor} b_i\) et \(R_{i} = a_i b_i\).
Circuit demi-additionneur (en S de P)
Circuit demi-additionneur avec porte XOR
Additionneur complet
Une addition binaire complète de deux arguments constitués de \(n\) bits procède du bit le moins significatif vers le bit le plus significatif, en additionnant à chaque étape trois bits: \(a_{i}\), \(b_{i}\) et \(r_{i-1}\) et en produisant une somme \(S_{i}\) et une retenue \(R_{i}\).
Diag-K pour \(S_i\)
Diag-K pour \(R_i\)
Les expressions simplifiées sont
\[S_{i} = a_i^\prime b_i^\prime r_{i-1} + a_i^\prime b_i r_{i-1}^\prime + a_i b_i^\prime r_{i-1}^\prime + a_i b_i r_{i-1}\] \[R_{i} = a_i b_i + a_i r_{i-1} + b_i r_{i-1}\]
Circuit additionneur complet pour \(S_i\)
Circuit additionneur complet pour \(R_i\)
Comme nous le disions précédemment, il est possible de combiner deux demi-additionneurs pour réaliser un additionneur complet, comme on peut le voir ici.
Circuit additionneur complet comportant deux demi-additionneurs et une porte OU